A sample from a digital pipe organ contains at least:
- an attack transient leading into
- a looped sustain block and
- a release which will be cross-faded into when the note is released.
The release cross-fade must be fast (otherwise it will not sound natural or transient details may be lost) and it must also be phase-aligned to the point where the cross-fade begins.
The necessity for phase alignment
Without phase aligning the release, disturbing artefacts will likely be introduced. The effects are different with short and long cross-fades but are always unpleasant.
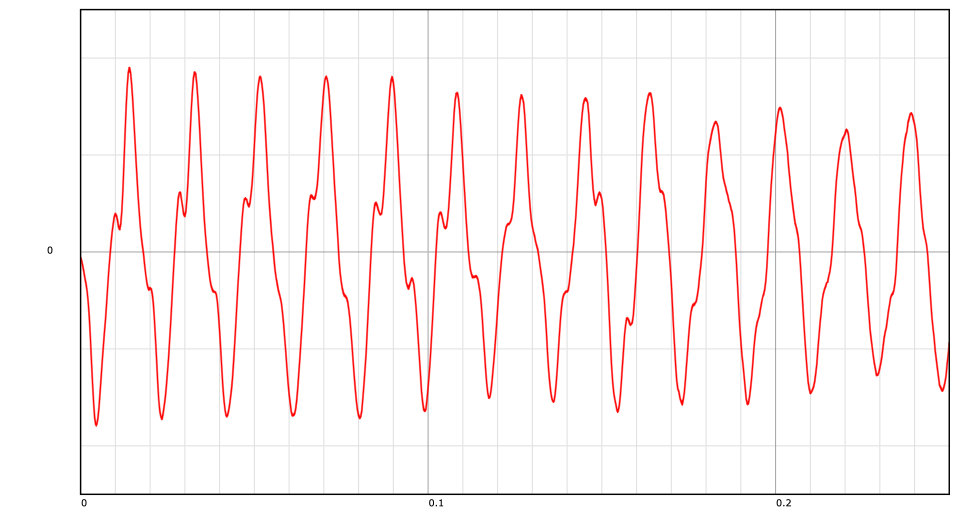
The following image shows an ideal cross-fade into a release sample. The crossfade begins at 0.1 seconds and lasts for 0.05 seconds. The release is aligned properly and the signal looks continuous.
The following image shows a bad release where the cross-fade is lagging an ideal release offset by half-a-period. Some cancellation occurs during the cross-fade and the result will either sound something like a “pluck” for long cross-fades or a “click” for short cross-fades.
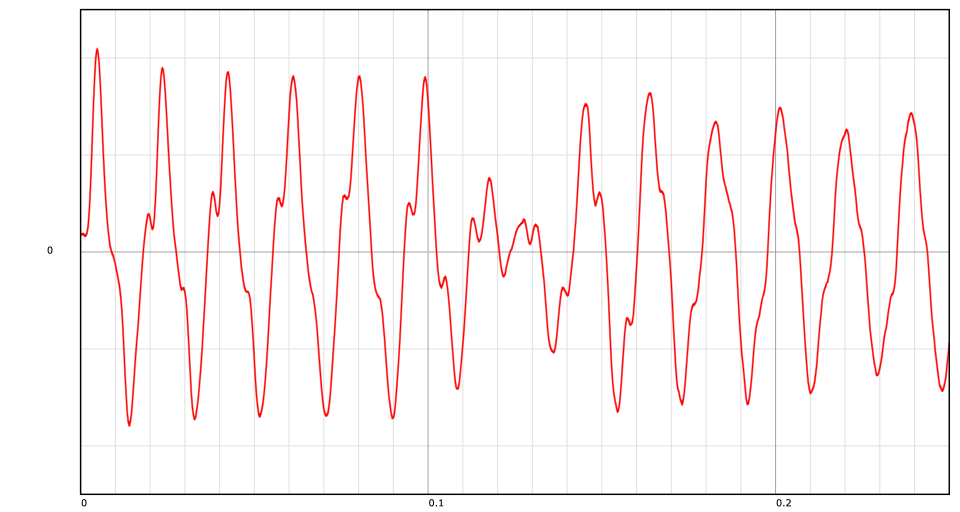
(The cross-fade used in generating the above data sets was a raised cosine - linear cross-fades can be used but will result in worse distortions).
The problem of aligning release cross-fades in virtual pipe organs is an interesting one. As an example: at the time of writing this article, release alignment in the GrandOrgue project is not particularly good; it uses a lookup-table taking the value and first-order estimated derivative (both quantised heavily) of the last sample of the last played block as keys. This is not optimal as a single sample says nothing about phase and the first-order derivative estimate could be completely incorrect in the presence of noise.
Another approach for handling release alignment
If the pitch a pipe was to be completely stable, known (\(f=\frac{1}{T}\)) and we knew one point where the release was perfectly aligned (\(t_r\)), we know that we could cross-fade into the start of the release at:
\[ \forall n \in \mathbb Z, t = t_r + T n \]
Hence, for any sample offset we could compute an offset into the release to cross-fade into.
In reality, pipe pitch wobbles around a bit and so the above would not strictly hold all the time - that being said, it is true for much of the time. If we could take a pipe sample and find all of the points where the release is aligned we could always find the best way to align the release.
It turns out that a simple way to do this is to find the cross-correlation of the attack and sustain segment with a short portion of the release. Taking the whole release would be problematic because as it decays it becomes less similar to the sustaining segment (which leads to an unhelpful correlation signal).
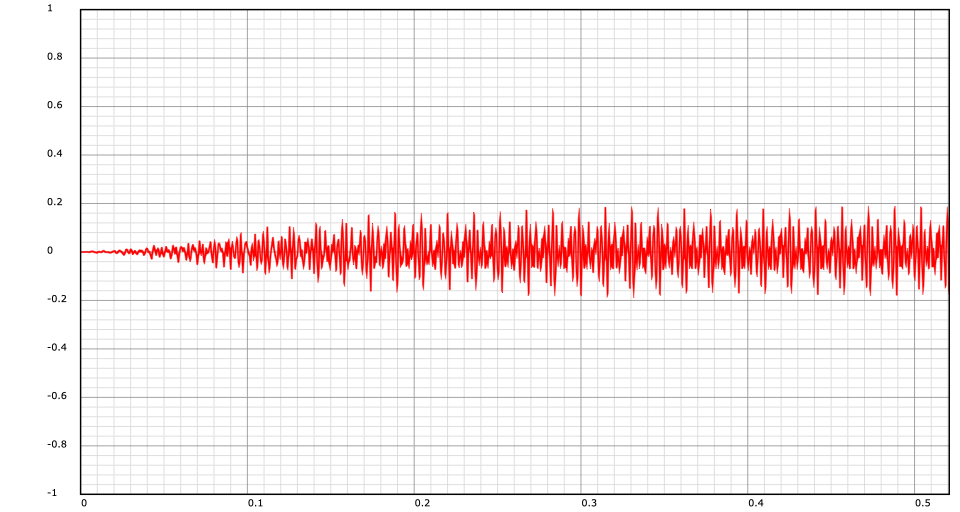
The above image shows the attack and some sustain of bottom-C of the St. Augustine's Closed Horn. This shows visually why single sample amplitude and derivative matching is a poor way to align releases. During one period of the closed horn, there are 14 zero crossings and 16 obvious zero crossings in the derivative. One sample gives hardly enough information.
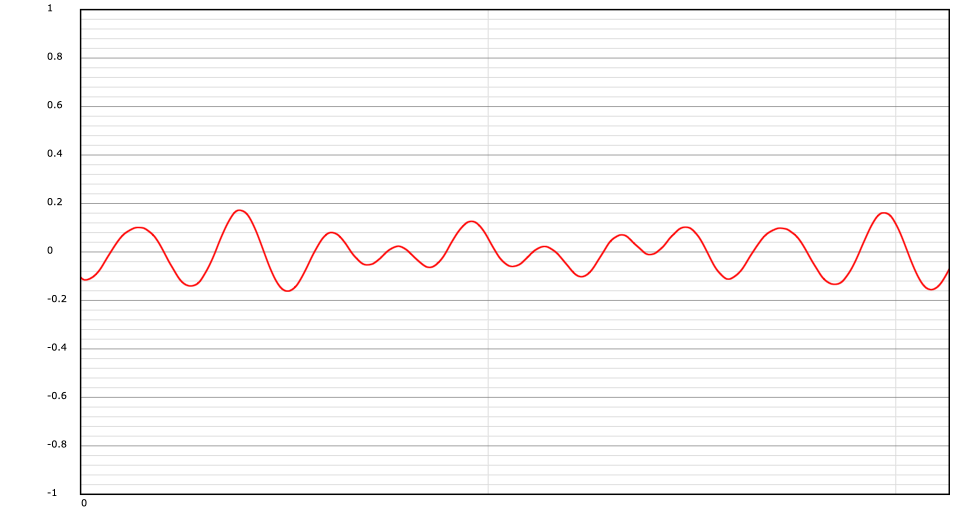
The above image shows a 1024 sample segment taken from the release marker of the same Closed Horn sample. It contains just over a single period of the horn.
The next image shows the cross-correlation of this release segment with the sample itself. My analysis program does correlation of the left and right channels and sums them to provide an overall correlation. Positive maximums correspond to points where the release will phase-align well. Minimums correspond to points where the signal has the least correlation to the release.
Using the correlation and a pitch guesstimate, we could construct a function which given any sample offset in the attack/sustain could produce an offset into the release which we should cross-fade into. This is for next time.